vector3
3D Vector library with meta functions
License: GPLv3
Usage
- Make your mod depends on
vector3; - Create vectors with
vector3(x, y, z); - See available methods below
All functions create new vectors so that the original vector is not modified. All the functions return the new vector so that operations can be chained easily.
Example:
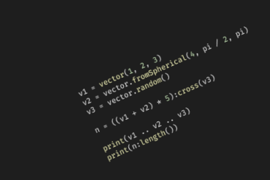
u = vector3(1, 2, 3)
v = vector3(4, 5, 6)
w = (5 * u + u:dot(v) * u:cross(v:scale(5))):norm()
Constructors
vector3(x, y, z)
Creates a new vector with components x, y and z. Components defaults to zero.
v0 = vector3() -- (0,0,0)
v1 = vector3(1,2,3) -- (1,2,3)
vector3.fromSpherical(r, theta, phi)
Creates a new vector from spherical coordinates. theta is the polar angle (from the upwards y axis), phi the azimut (counting clockwise around y, starting from x), and r the radius. Default values are r=1, theta=pi/2, phi=0.
v2 = vector3.fromSpherical(10, math.pi / 2, math.pi) -- (10, 0, 0)
vector3.fromCylindrical(r, phi, y)
Creates a new vector from cylindrical coordinates. r is the radius, phi is the azimut angle (counting clockwise around y, starting from x) and y the height. Default values are r=1, phi=0 and y=1.
v21 = vector3.fromCylindrical(10, math.pi / 2, 5) -- (0, 5, 10)
vector3.fromPolar(r, phi)
Creates a new vector from polar coordinates. r is the radius and phi the angle (counting clockwise around y, starting from x), and . Default values are r=1 and phi=0.
v22 = vector3.fromPolar(6, - math.pi / 2) -- (0, 0, -6)
vector3.srandom(a, b)
Creates a vector with random spherical coordinates and with the radius drawn at random between a and b
v3 = vector3.srandom()
vector3.crandom(a, b, c, d)
Creates a vector with random cylindrical coordinates. The radius is drawn at random between a and b and the height between c and d
v31 = vector3.crandom(0, 10, 5, 15)
vector3.prandom(a, b)
Creates a vector with random polar coordinates and with the radius drawn at random between a and b
v32 = vector3.prandom()
Constants
vector3.zero = vector3(0, 0, 0)
vector3.one = vector3(1, 1, 1)
vector3.none = -vector3(1, 1, 1)
vector3.x = vector3(1, 0, 0)
vector3.y = vector3(0, 1, 0)
vector3.z = vector3(0, 0, 1)
vector3.xy = vector3(1, 1, 0)
vector3.yz = vector3(0, 1, 1)
vector3.xz = vector3(1, 0, 1)
vector3.nx = -vector3(1, 0, 0)
vector3.ny = -vector3(0, 1, 0)
vector3.nz = -vector3(0, 0, 1)
vector3.nxy = -vector3(1, 1, 0)
vector3.nyz = -vector3(0, 1, 1)
vector3.nxz = -vector3(1, 0, 1)
Meta functions
Allows to print a vector.
print(v1)
concatenation
Allows to create strings from vector concatenation.
print(v1 .. v2 .. v3)
negative
Returns the opposite vector.
v5 = -v1
equality
Return true if two vectors have their components equals
v1 == v2
addition
Return the sum of two vectors component wise. If one argument is a number then this number is added to each component of the vector.
v1 + v2
v1 + 10
subtraction
Return the difference of two vectors component wise. If one argument is a number then this number is subtracted to each component of the vector.
v1 - v2
v1 - 1
multiplication
Return the product of two vectors component wise. If one argument is a number then each component of the vector is multiplied by this number.
v1 * v2
v1 * 10
division
Return the division of two vectors component wise. If one argument is a number then each component of the vector is divided by this number.
v1 / v3
v1 / 10
Functions
clone()
Return a new vector which is a copy of the initial vector.
v4 = v1:clone()
length()
Returns the magnitude of the vector.
v3:length()
norm()
Return the corresponding normalized vector (with magnitude one).
v3:norm()
scale(mag)
Return a new vector which is scaled to magnitude mag
v1:scale(10)
limit(max)
Returns a new vector which is scaled to magnitude max if its magnitude if greater than max.
vector3(10, 20, 30):limit(5)
vector3(1, 2, 3):limit(5)
floor()
Return a new vector with the components floored.
v3:floor()
round()
Return a new vector with the components rounded to the closest integer.
v3:round()
set(x, y, z)
Return a new vector with components x,y and z. If a parameter is nil then the corresponding component is unchanged.
v1:set(4, nil, 7)
offset(a, b, c)
Return a new vector with components x, y, z offset by a, b and c. If a parameter is nil the corresponding component is unchanged.
v2:offset(-1, 3, 2)
apply(f)
Return a new vector with the function f applied to its components.
v2:apply(function(x) return x * x end)
dist(b)
Returns the distance between the current vector and b (as if they were representing points).
v1:dist(v2)
dot(b)
Returns the dot product of the current vector and b.
v1:dot(v2)
cross(b)
Returns a vector which is the cross product of the current vector and b.
v1:cross(v2)
rotate_around(axis, angle)
Returns a new vector which is the current vector rotated around axis with angle.
axis = vector3(0, 1, 0)
v2:rotate_around(axis, math.pi)
unpack()
Returns the unpacked components of the current vector.
x, y, z = v1:unpack()
print(x)
print(y)
print(z)